题意

cft

有这样一个六边形坐标系，并给了六个移动方向C1-6。

cf2

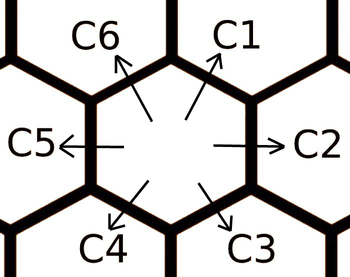
输入给定目标坐标xy，并且给定C1-6每个方向的费用，求从(0,0)到(x,y)的最小费用。

思路

我们可以发现，要进行一次C2的移动，可以通过一次C1和一次C3合成，同理如果向进行一次C1移动，也可以通过C6和C2进行合成。所以我们先进行一次类似最短路的操作，如果一个方向x的费用比它左右x+1,x-1相加的还要多，则需要把这个费用替换。

这样操作之后，我们可以得到如果要从(0,0)到(x,y)，最多只需要走用到两个方向。（注意，这里的方向经过了之前的操作，其实和一开始的移动是不一样的）

之后我们枚举选哪两种方向就行了。我比赛的时候选择的方法比较傻逼，是给定一个坐标(x,y)，我先枚举：要先搞定x还是先搞定y，然后判断x(或y)变成0之后，需要用哪一个方向，套了两重循环，比较不科学。后来看了大佬们的代码发现有效率更高更好写的方法。

代码

比赛时的代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
#include<cmath>
using namespace std;

template<class T>inline void read(T &x){x=0;char o,f=1;while(o=getchar(),o<48)if(o==45)f=-f;do x=(x<<3)+(x<<1)+(o^48);while(o=getchar(),o>47);x*=f;}
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
#define ll long long
#define ull unsigned long long
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=b;i--)
#define log(x) (31-__builtin_clz(x))
#define INF 0x3f3f3f3f
#define int ll
ll gcd(ll a,ll b){ while(b^=a^=b^=a%=b); return a; }
//#define INF 0x7fffffff
int dir[6][2] = {1,1,0,1, -1,0,-1,-1, 0,-1,1,0};
ll c[6];
ll tx,ty;
ll res;
inline ll cd(int x){ return c[ (x+6)%6 ]; }
inline bool th(ll a,ll b){//判断同号
	if(a==b&&a==0) return 1;
	else if(a>0&&b>0) return 1;
	else if(a<0&&b<0) return 1;
	return 0;
}
void solve(){
	res = 0;
	cin>>tx>>ty;
	rep(i,0,5) cin>>c[i];//费用;
	rep(i,0,5){//最短路思想
		if(cd(i-1)+cd(i+1)<cd(i)) c[i] = cd(i-1)+cd(i+1);
	}
	ll minn = 1LL<<62;
	//我懂了，最多只需要两种方向。
	//先把tx弄到相同的方案
	//先搞x再搞y的情况
	rep(i,0,5){
		res = 0;
		ll tty = ty;ll ttx = tx;
		if(dir[i][0]==0) continue;
		if(th(dir[i][0],ttx)||ttx==0){
			ll tim = abs(ttx);
			tty -= tim*dir[i][1];
			ttx = 0;
			res += c[i]*tim;
			rep(j,0,5){
				if(dir[j][0]!=0) continue;
				if(dir[j][1]==0) continue;
				if(th(dir[j][1],tty)||tty==0){
					ll tim = abs(tty);
					ll res2 = res + c[j]*tim;
					minn = min(minn,res2);
					//cout<<i<<' '<<j<<':'<<res<<' '<<res2<<endl;
				}
			}
		}
	}
	//先搞y再搞x
	rep(i,0,5){
		res = 0;
		ll tty = ty;ll ttx = tx;
		if(dir[i][1]==0) continue;
		if(th(dir[i][1],tty)||tty==0){
			ll tim = abs(tty);
			ttx -= tim*dir[i][0];
			tty = 0;
			res += c[i]*tim;
			rep(j,0,5){
				if(dir[j][1]!=0) continue;
				if(dir[j][0]==0) continue;
				if(th(dir[j][0],ttx)||ttx==0){
					ll tim = abs(ttx);
					ll res2 = res + c[j]*tim;
					minn = min(minn,res2);
					//cout<<i<<' '<<j<<':'<<res<<' '<<res2<<endl;
				}
			}
		}
	}
	cout<<minn<<endl;
}

signed main(){
	int z;
	cin>>z;
	while(z--) solve();
}