理论部分
是这篇博客的学习笔记(自己看的整理总结,侵删)
https://www.cnblogs.com/zwfymqz/p/8244902.html
https://www.luogu.com.cn/blog/attack/solution-p3803
神犇博客
看完了才发现B站上有个特别好的视频BV1Y7411W73U
非常好非常好非常好非常牛逼非常牛逼非常牛逼这个视频
多项式知识
负数运算法则
$(a+bi)*(c+di)=ac+adi+bci-bd=(ac-bd)+(bc+ad)i$
单位根
复平面上把这个圆分成n等分的终点,角度最小的哪一个就是n次单位根,记作$w_{n}$
单位根$w_{n}^{k}$的数值即$\cos(k\cdot\frac{2\pi}{n})+\sin(k\cdot\frac{2\pi}{n})i$
有性质$w^{k}{n}=w^{2k}{2n}$,易证。
FFT
拆两半
给多项式
$A(x)=a_{0}+a_{1}x+a_{2}x^{2}+\dots+a_{n-2}x^{n-2}+a_{n-1}x^{n-1}$
按照奇次偶次项分,得到
$A(x)=(a_{0}+a_{2}x^{2}\dots a_{n-2}x^{n-2}) + (a_{1}x\dots a_{n-1}x^{n-1})$
则有$A(x) = A_1(x^{2}) + x A_2(x^{2})$
把$w_n ^k (k< \frac{n}{2})$带入有
$A( w_{n} ^{k} ) = A_{1}( w_{n} ^{2k}) + w_{n} ^{k} A_2( w_{n} ^{2k})$
$= A_1(w_{ \frac{n}{2}}^{k}) + w_n ^k A_2(w_{ \frac{n}{2}}^{k})$式子1
把$w_{n} ^{k + \frac{n}{2}}$带入得到
$A( w_n ^{k + \frac{n}{2} } ) = A_1( (w_n ^{k + \frac{n}{2} })^2 ) + w_n ^{k + \frac{n}{2} } A_2( (w_n ^{k + \frac{n}{2} })^2 )$
$= A_1(w_{n}^{2k+n}) - w_n ^k A_2(w_{n}^{2k+n})$//+号因为正好去掉一个$\pi$所以变成-了,里面把平方去了
$= A_1(w_{n}^{2k}) - w_n ^k A_2(w_{n}^{2k})$//n可以去掉
$= A_1(w_{ \frac{n}{2}}^{k}) - w_n ^k A_2(w_{ \frac{n}{2}}^{k})$式子2
处理一个的同时得到另外一个
这时候可以找到规律,两个式子只有一个常数项不同(也只是正负号的区别)
所以算完式子1,只需要$O(1)$ 就有式子2的结果了
第一个式子$k$在取遍$ [0,\frac{n}{2}−1]$ 时,第二个式子也跟着取了$k+ \frac{n}{2}$即$[\frac{n}{2},n-1]$
问题的复杂度直接缩小一半。
这之后直接递归处理,当多项式只剩下一个项的时候返回就行了
复杂度
$O(nlogn)$
快速傅里叶逆变换
上面已经变成点值表示法了,之后还要学怎么从点值变回系数表示法
把点值作为系数得到B(x)
$(y_0,y_1,y_2,\dots,y_{n−1})$为$(a_0,a_1,a_2,\dots,a_{n-1})$的傅里叶变换
设$c_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i$即$c_k$是k单位根的
$B(x)=y_0,y_1x,y_2x^2,\dots,y_{n-1}x^{n-1}$
$k = 1,2,\dots,n-1$
在$x= \omega_n^{0},\omega_n^{-1},\omega_n^{-2},\dots,\omega_{n-1}^{-(n-1)}$这$B(x)$这n个点上的点值
Ck变一下形
$c_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i$
$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^i)^j)(\omega_n^{-k})^i$
$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^j)^i)(\omega_n^{-k})^i$//为了和后面的i次一样,这里把i和j交换一下
$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^j)^i(\omega_n^{-k})^i)$
$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^j)^i(\omega_n^{-k})^i$
$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j(\omega_n^{j-k})^i$//把同样是i次的两个合并了
$=\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i)$
先简化成S(x)讨论
接下来设$S(x) = \sum_{i=0}^{n-1} x^i$即从0到n-1次的x相加
即 $S(x) = \sum_{i=0}^{n-1} (\omega_{n}^{k})^i$
带入$\omega_n^k$时,如果$k = 0$时显然有$S(\omega_{n}^{k}) = n$
$k != 0$时,这时候该怎么算
用类似高中数列的方法,叫啥来着好像叫?反正乘上去做差就完了
$\omega_{n}^{k}*S(x) - S(x)$
$=(\omega_n^k)^n-1$
变形得到
$S(x) = \frac{1-1}{\omega_n^k -1}$//这里中间省掉了好多的步骤,反正推一下也简单的
所以可以看出来$k!=0$时,$S(x) = 0$
讨论完S(x),回去看之前的Ck
结合之前$ S(x) $的结论,可以知道,$j-k != 0$时,$c_k = 0$
即只有$j=k$的时候才不是0,而是n。
$\sum_{j=0}^{n-1}a_j(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i)$中后面那一项其实就是n,还是比较好理解的
所以有$c_k = n*a_k$
$a_k = \frac{c_k}{n}$
这样就得到了点值和系数之间的关系
其实从点值到系数的这一步也是通过之前的FFT去实现的,非常牛逼
实现部分
AC代码
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
inline int read(){
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
const int MAXN = 3e6+5;
const double Pi = acos(-1.0);
struct cplx{//手写负数complex用起来会更快
double x,y;
cplx(double x=0,double y=0):x(x),y(y){}
friend cplx operator + (cplx a,cplx b){return cplx(a.x+b.x,a.y+b.y);}
friend cplx operator - (cplx a,cplx b){return cplx(a.x-b.x,a.y-b.y);}
friend cplx operator * (cplx a,cplx b){return cplx(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
}a[MAXN],b[MAXN];
void FFT(int limit,cplx *a,int type){//limit记录项数
if(limit==1) return;//只有一个常数项结束递归(即只剩下0次的)
cplx a1[limit>>1],a2[limit>>1];//按照奇偶分组
for(int i=0;i<limit;i+=2)
a1[i>>1] = a[i],a2[i>>1] = a[i+1];
FFT(limit>>1,a1,type);
FFT(limit>>1,a2,type);
cplx Wn(cos(2*Pi/limit),type*sin(2*Pi/limit));//单位根
//这里type挺重要的,反变换的时候用-1,因为是-k
cplx w(1,0);//一会儿算单位根幂的时候用w存
for(int i=0;i<(limit>>1);i++,w=w*Wn){//w相当于公式中的w_n^k
a[i]=a1[i]+w*a2[i];//偶
a[i+(limit>>1)]=a1[i]-w*a2[i];//O(1)算另外一部分
}
}
int main(){
int n=read(),m=read();
rep(i,0,n) a[i].x=read();
rep(i,0,m) b[i].x=read();
int limit = 1;
while(limit<=n+m) limit<<=1;//这里非常精髓
//把长度补到2的幂,这样就不用考虑%2余数的情况
//而且不必担心高次项的系数,因为默认为0
FFT(limit,a,1);
FFT(limit,b,1);
//1表示FFT,-1则是反变换
rep(i,0,limit) a[i] = a[i]*b[i];//转换为点值后直接相乘
FFT(limit,a,-1);//现在变回去
rep(i,0,n+m) printf("%d ",(int)(a[i].x/limit+0.5));//还要除以n的
printf("\n");
}
//P3803 【模板】多项式乘法(FFT)
//https://www.luogu.com.cn/problem/P3803大佬笔误
发现大佬的笔误在拆分奇偶的地方。
complex a1[limit>>1],a2[limit>>1];
for(int i=0;i<=limit;i+=2)//根据下标的奇偶性分类
a1[i>>1]=a[i],a2[i>>1]=a[i+1];这里显然会出现数组越界的情况,要么数组再开大点,要么<=limit改成<limit。验证过两种都行,不过显然第二种会比较好一点。
算法优化
蝴蝶操作
优化计算了两次的部分
上面在计算$A_1$和$A_2$时:
$A( w_{n} ^{k} ) =A_1(w_{ \frac{n}{2}}^{k}) + w_n ^k A_2(w_{ \frac{n}{2}}^{k})$式子1
$A( w_n ^{k + \frac{n}{2} } )= A_1(w_{ \frac{n}{2}}^{k}) - w_n ^k A_2(w_{ \frac{n}{2}}^{k})$式子2
前一项完全相同,后一项也仅仅是相差一个正负号。但是在之前的代码里我们这一步计算了两次。
for(int i=0;i<(limit>>1);i++,w=w*Wn){//w相当于公式中的w_n^k
a[i]=a1[i]+w*a2[i];//偶
a[i+(limit>>1)]=a1[i]-w*a2[i];//O(1)算另外一部分
}是吧,这里显然是可以优化的
cplx tmp;
for(int i=0;i<(limit>>1);i++,w=w*Wn){//w相当于公式中的w_n^k
tmp = w*a2[i];//蝴蝶操作
a[i]=a1[i]+tmp;//偶
a[i+(limit>>1)]=a1[i]-tmp;//O(1)算另外一部分
}迭代实现FFT
观察多次奇偶拆分后下标的变化
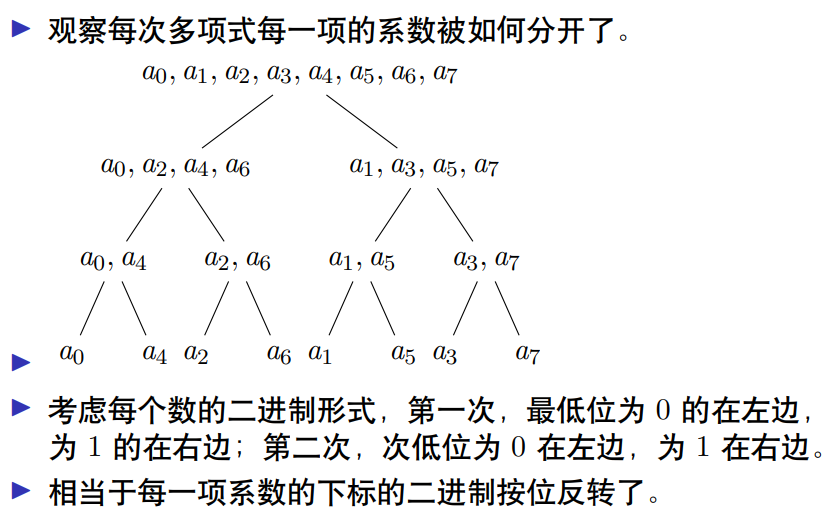
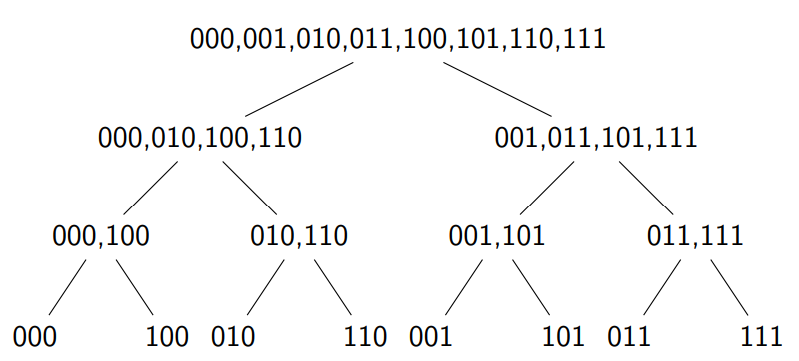
是按照位逆序置换排列的,$O(n)$来预处理
如何O(n)预处理位逆序置换

有递推式rev[i] = (rev[i>>1]>>1) | ((i&1)<<(len-1))
解释一下这段代码:
- 如图中所说的,每组数字的位逆序置换的后面几位都是上一级问题的子问题的解
1为100,2为010 而 4为001,可以看到这一层一层网上推的时候就是把上一层的往后移动一位
最前面的(rev[i>>1]>>1)中rev[i>>1]是上一级子问题的解,最后再>>1是往后移动一位
- 第一位即最底层的子问题——模2余1还是余0,确定首位是1还是0
(i&1)取来下标的最后一位,<<(len-1)把这个数字移动到首位
按照位逆序从底层往上进行蝴蝶操作
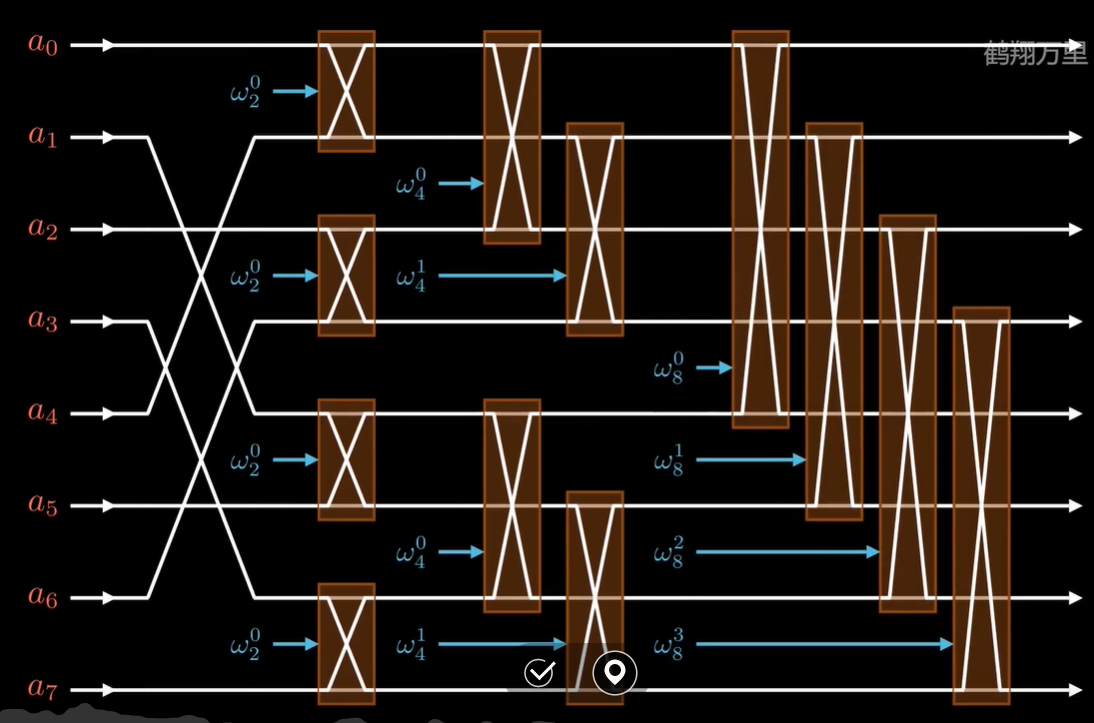
第二层是2个一组,第三层是4个一组每组里面,即每层每组的个数m为1<<dep
枚举m的数值之后就是每层分成limit/m个m个元素的组
外面一个循环:k表示每个m元组的起始位置,每次k要+=m;
再来一个循环,j从0到m/2 -1循环:
这样一来,就是k+j和k+j+m/2两两进行蝴蝶操作
代码实现
(基本上就是抄BV1Y7411W73U的,这个视频非常nice)
之前一直错,结果发现是错在这个地方
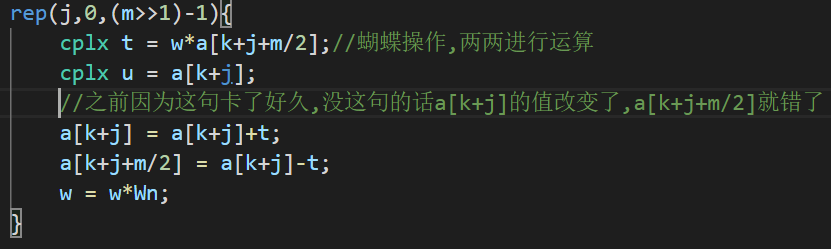
a[k+j]的数值已经更改后,算a[k+j+m/2]就有问题
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
inline int read(){
char c=getchar();int x=0,f=1;
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
const int MAXN = 3e6+5;
const double Pi = acos(-1.0);
struct cplx{//手写负数complex用起来会更快
double x,y;
cplx(double x=0,double y=0):x(x),y(y){}
friend cplx operator + (cplx a,cplx b){return cplx(a.x+b.x,a.y+b.y);}
friend cplx operator - (cplx a,cplx b){return cplx(a.x-b.x,a.y-b.y);}
friend cplx operator * (cplx a,cplx b){return cplx(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
}a[MAXN],b[MAXN];
void FFT(int limit,cplx *a,int type){//limit记录项数
if(limit==1) return;//只有一个常数项结束递归(即只剩下0次的)
cplx a1[limit>>1],a2[limit>>1];//按照奇偶分组
for(int i=0;i<limit;i+=2)
a1[i>>1] = a[i],a2[i>>1] = a[i+1];
FFT(limit>>1,a1,type);
FFT(limit>>1,a2,type);
cplx Wn(cos(2*Pi/limit),type*sin(2*Pi/limit));//单位根
//这里type挺重要的,反变换的时候用-1,因为是-k
cplx w(1,0);//一会儿算单位根幂的时候用w存
cplx tmp;
for(int i=0;i<(limit>>1);i++,w=w*Wn){//w相当于公式中的w_n^k
tmp = w*a2[i];//蝴蝶操作
a[i]=a1[i]+tmp;//偶
a[i+(limit>>1)]=a1[i]-tmp;//O(1)算另外一部分
}
}
int main(){
int n=read(),m=read();
rep(i,0,n) a[i].x=read();
rep(i,0,m) b[i].x=read();
int limit = 1;
while(limit<=n+m) limit<<=1;//这里非常精髓
//把长度补到2的幂,这样就不用考虑%2余数的情况
//而且不必担心高次项的系数,因为默认为0
FFT(limit,a,1);
FFT(limit,b,1);
//1表示FFT,-1则是反变换
rep(i,0,limit) a[i] = a[i]*b[i];//转换为点值后直接相乘
FFT(limit,a,-1);//现在变回去
rep(i,0,n+m) printf("%d ",(int)(a[i].x/limit+0.5));//还要除以n的
printf("\n");
}
//P3803 【模板】多项式乘法(FFT)
//https://www.luogu.com.cn/problem/P3803


