多校补题记录
n个区间分k组,使每组区间的并集长度之和最大
牛客2-G-League of Legends 【单调队列优化DP】
G-League of Legends_2021牛客暑期多校训练营2 (nowcoder.com)
题意:给n,k(5000),有n个成员要被分成k组,每组对答案的贡献为:所有组员空闲时间[ai,bi)的并集的长度。求最大的答案。
解:把所有的线段分成两个集合,“大边”和“小边”,如果一个线段能够完整包含另一条线段,那这个边是“大边”,剩余的边为“小边”。
//O(n)处理大边小边
int minr = INF;
sort(a+1,a+1+n,cmp);//这里第一关键字是ft小,第二关键字是sd大
repb(i,n,1){//分成大小区间
if(a[i].sd>=minr) da[++cd] = a[i].sd-a[i].ft;//大区间只记录长度
else minr = a[i].sd,xi[++cx] = a[i];
}一条大边只有两种去处:一种是单独成组,贡献=长度。另一种是跟随某条能被它完全包含的“小边”进入同一组,则对答案不造成影响。
对小边,在对pair排序后,i位置一定满足$L_i \geq L_{i-1}$且$R_i \geq R_{i-1}$。
因此我们只需要讨论小边的答案,最后枚举使用大边的数量即可。一段连续的小边$(i,j)$如果要放在同一组,一定满足$L_j>R_i $,而且这么成一组的贡献就是$L_j-R_i$。
设$DP_{i,j}$为前i组用了j个人的最优解。显然有公式$DP_{i,j} = DP_{i-1,k} + (R_{k+1}-L{j})$,这么以来就有了$n^3$的做法。之后考虑使用优先队列优化,把$DP_{i,j} = DP_{i-1,k} + (R_{k+1}-L{j})$中的$DP_{i-1,k} + R_{k+1}$推入队列即可。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
template<class T>inline void read(T &x){x=0;char o,f=1;while(o=getchar(),o<48)if(o==45)f=-f;do x=(x<<3)+(x<<1)+(o^48);while(o=getchar(),o>47);x*=f;}
#define ll long long
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=(b);i--)
#define INF 0x3f3f3f3f
typedef pair<int,int> pii;
#define ft first
#define sd second
#define mkp make_pair
const int MAXN = 5050;
pii a[MAXN],xi[MAXN];//小边
int da[MAXN];//大边
int cd,cx;//记数
int n,m;//n个人分m组
int dp[MAXN][MAXN];//分成i组,用前j个
pii q[MAXN];//对于每个1<=i<=m分配一条优先队列
//优先队列,ft存dp[i][k] + xi[k].sd,sd存 xi[k].sd
int st,ed;
bool cmp(pii a,pii b){
if(a.ft==b.ft) return a.sd>b.sd;
return a.ft<b.ft;
}
void solve(){
cin>>n>>m;//分成m组
rep(i,1,n)
cin>>a[i].ft>>a[i].sd;
int minr = INF;
sort(a+1,a+1+n,cmp);
repb(i,n,1){//分成大小区间
if(a[i].sd>=minr) da[++cd] = a[i].sd-a[i].ft;//大区间只记录长度
else minr = a[i].sd,xi[++cx] = a[i];
}
sort(xi+1,xi+1+cx);
dp[0][0] = 0;//要特殊处理一下
rep(i,1,m){
st=1,ed=0;
rep(j,i,cx){
if((i==1&&j==1)||dp[i-1][j-1]!=0){
while(st<=ed&&q[ed].ft<=dp[i-1][j-1]+xi[j].sd) ed--;//pop back;
q[++ed] = mkp(dp[i-1][j-1]+xi[j].sd,xi[j].sd);
}
while(st<=ed&&q[st].sd<=xi[j].ft) st++;//pop front
if(st<=ed)
dp[i][j] = q[st].ft - xi[j].ft;//dp[i][k]+xi[k].sd - xi[j].ft
}
}
//接下来枚举前缀和
sort(da+1,da+1+cd,greater<int>());
cd = min(cd,m);
int res = 0;
int sum = 0;
rep(j,0,m){//前j个大区间单独成组
sum += da[j];//做前缀和
if(dp[m-j][cx]==0) continue;//无效值
res = max(res,dp[m-j][cx]+sum);
}
cout<<res<<endl;
}
int main(){
//freopen("in.txt","r",stdin);
solve();
}注意单调队列实现的细节。一开始一直wa,因为是要满足$k<j$的,所以只有在计算到$DP_{i,j}$时,才能把$DP_{i-1,j-1}+R_j$推进来。
把字符串分成两段,问有多少失配数<=k的子串
杭电多校5 Another String【滑动窗口,差分】
题意:给一个长3000的串n,和允许最大失配数(距离)k,问对于每个分界点i,左右两侧有多少对距离小于等于k的子串。
这个分界点$i$,题目定义的是左半边的最后一个字符,即左半边为$s[1,i]$右半边为$s[i+1,n]$。
我写的时候定$i$为右半边的第一个字符,即左半边为$s[1,i-1]$,右半边为$s[i,n]$。
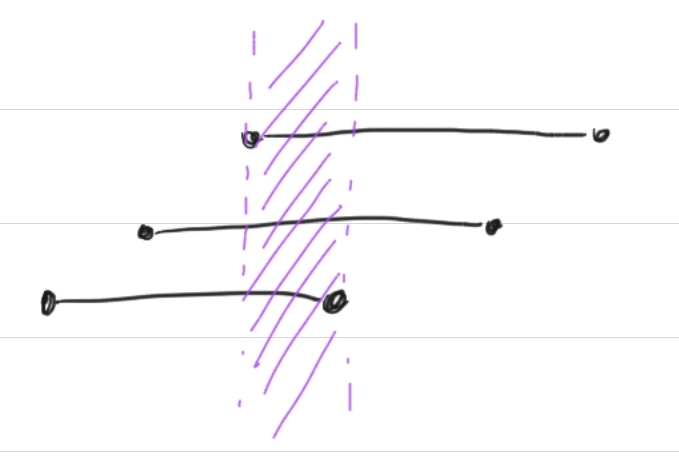
解:第一层枚举两个滑动窗口的间距d,然后在里面用for循环枚举$l$,对于每个$l$,使$r$一直增加得到最大的且距离不超过$k$的子串。
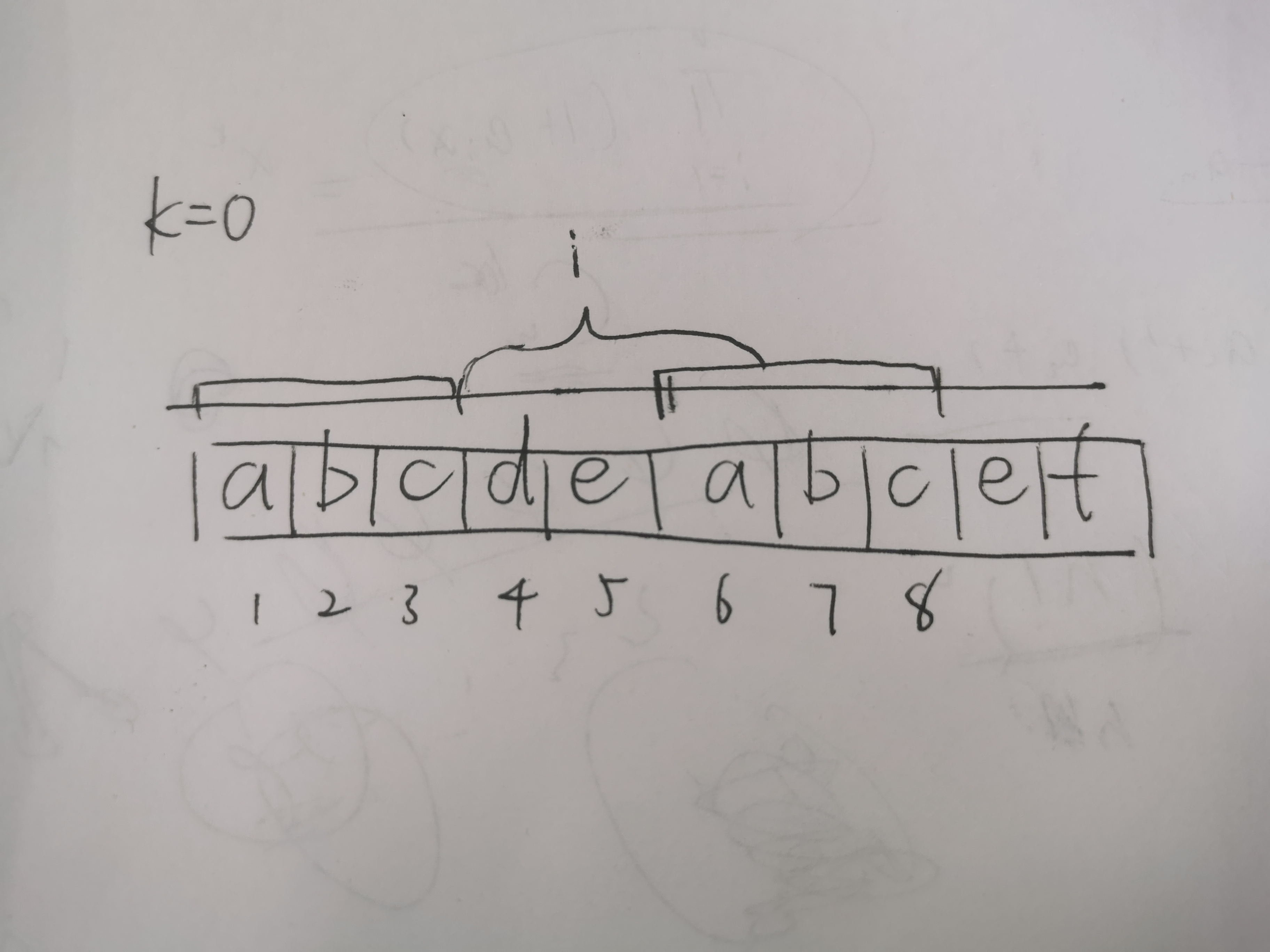
如图,可以发现对于这一对匹配串,可以选择的分界点$i$从$4$到$6$,在结果上,对这一段的$res[4]$到$res[6]$,都要$+1$,可以用差分数组实现。
但是这样只是讨论到“最长”的情况,对于每个l而言,不仅仅是这个最大的r可以使得串s[l,r]与串$s[d+l-1,d+r-1]$匹配,对于其他的$l\leq x\leq r$,显然对于串$s[l,x]$和$s[l+d-1,x+d-1]$也满足条件,故我们在图上标出这些满足条件的子串:
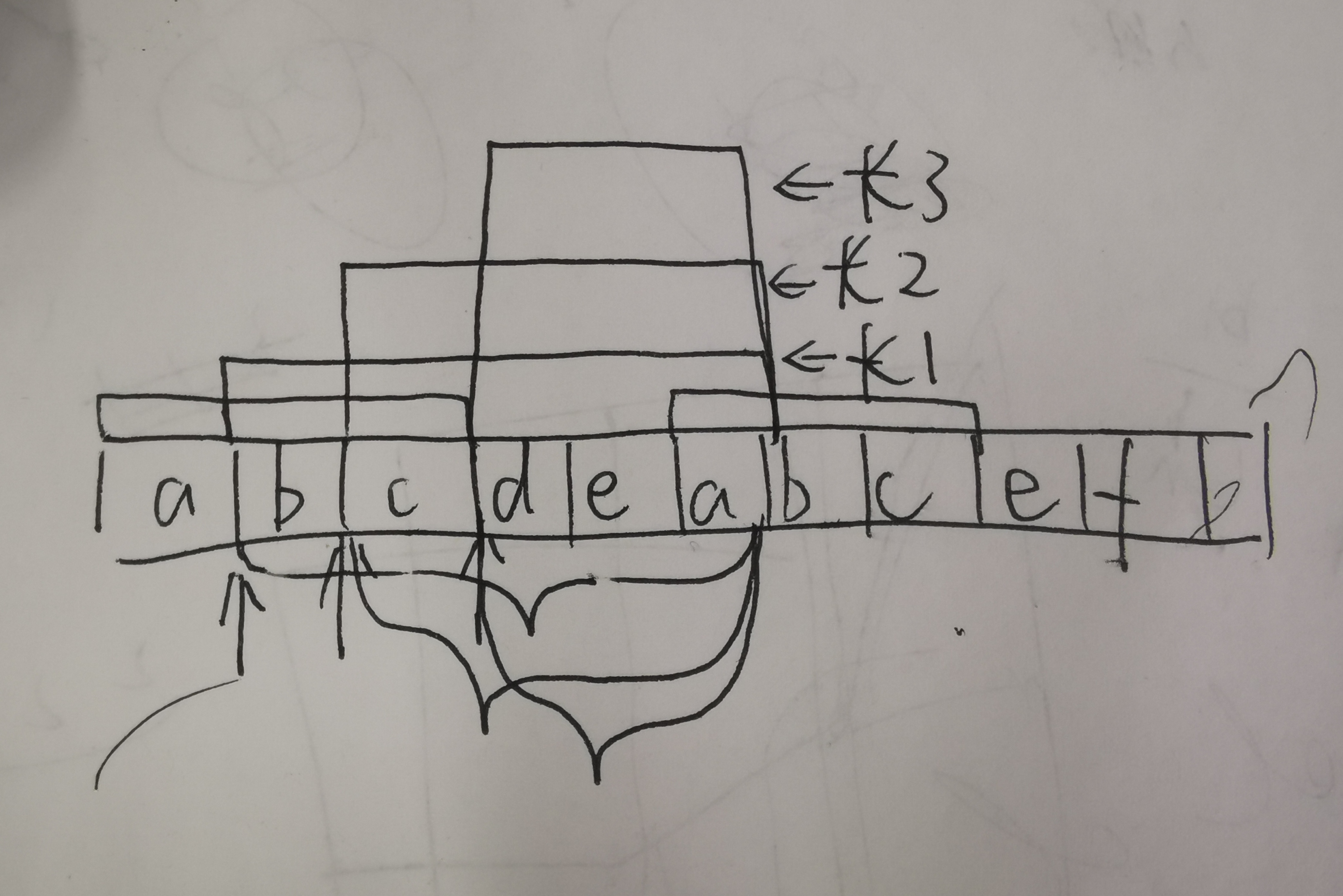
- 可以发现,这对串的结束点x从后往前移动,分别有长度为1,2,3的三对匹配串。长度为1的串’a’有符合条件的分界点$i\in [2,6]$,长度为2的串’ab’有符合条件的分界点$i\in [3,6]$,长度为3的串’abc’有符合条件的分界点$i\in[4,6]$。可以发现,对答案的贡献为一个梯型。
- 我们用差分数组实现,要构造这样的梯形,需要在差分数组的cf[2,3,4]处+1,cf[7]处-3。但是对于这个梯形比较长的时候,修改差分数组的复杂度也变成了$O(n)$,故需要再造一个差分数组的差分数组cf2,原本的cf[2,3,4]+=1,可以变成cf[2]+=1,cf[5]-=1。
赛中这题其实已经写的七七八八了,最后发现,对于第一层枚举的间距d,我并没有把这个理解成间距,而是理解成另外一个分界点x,想着滑窗的时候,不能让左边的l和r超过这个分界点x,实际上完全是可以的,不然会漏掉很多情况。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
template<class T>inline void read(T &x){x=0;char o,f=1;while(o=getchar(),o<48)if(o==45)f=-f;do x=(x<<3)+(x<<1)+(o^48);while(o=getchar(),o>47);x*=f;}
#define ll long long
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=(b);i--)
#define INF 0x3f3f3f3f
ll gcd(ll a,ll b){ while(b^=a^=b^=a%=b); return a; }
int n,k;
string s;
const int MAXN = 3090;
ll cf1[MAXN],cf2[MAXN];
void solve(){
cin>>n>>k;
rep(i,1,n) cf1[i]=cf2[i]=0;
cin>>s;
s = ' '+s;
rep(fj,2,n){
int nowdis = 0;
int rb = 0;
rep(lb,1,n){
if(fj+lb-1>n) break;
while(rb+1<fj+lb-1&&fj+rb<=n&&nowdis+(s[rb+1]!=s[fj+rb])<=k){
rb++;
nowdis += s[rb]!=s[fj+rb-1];
}
nowdis -= (s[lb]!=s[fj+lb-1]);
cf1[lb+1]++;cf1[rb+2]--;
cf2[fj+lb]-=rb-lb+1;
}
}
ll now = 0;
rep(i,1,n){
now += cf1[i];
cf2[i] += now;
}
now = cf2[1];
rep(i,2,n){
now += cf2[i];
cout<<now<<endl;
}
}
int main(){
int z;
cin>>z;
while(z--) solve();
}图上选边,使两端点权-1,问最少步数
牛客多校9 J-Jam
J-Jam_2021牛客暑期多校训练营9 (nowcoder.com)
题意:有十字路口,每个路口有三个方向,每个时间点的安排不能使两条路线交叉,问最少需要多少个时间可以让十字路口的车都走完。(每个路口每个方向的车Ci,j<=100)
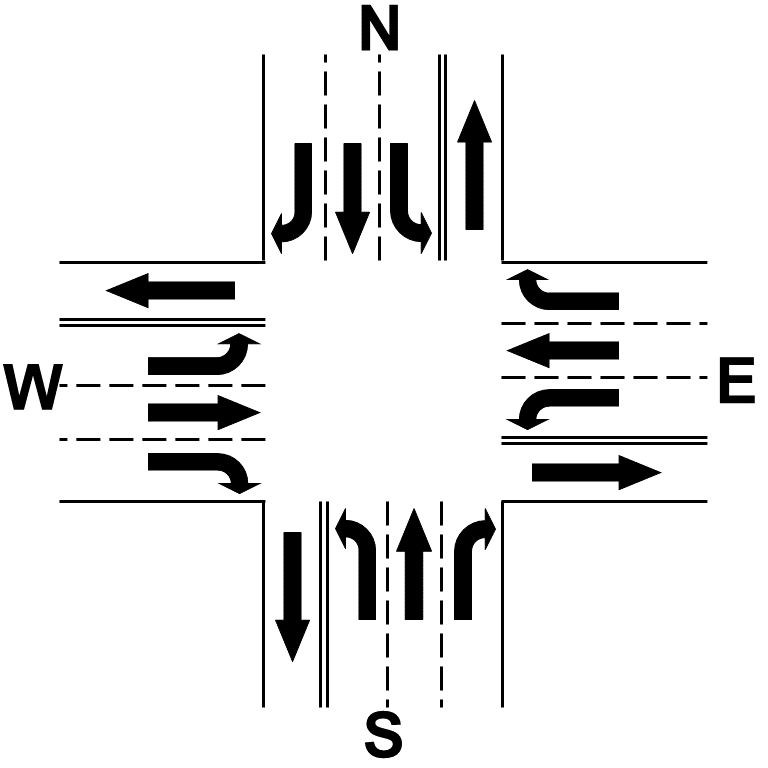
解:这题可以用带花树写,对每个车建点,之后跑图上的最大匹配。但是我们赛中写的是网络流。
首先可以发现,每个路口向右走的车辆可以独立出来,因为向右走是不与其他方向冲突点。
这样一来,可以把每方位的两种方向都拉出来,转变成了:”给定一张图,每次可以选择一条边,使得两端点权值各-1,问最少操作多少次使点权全部清空?”
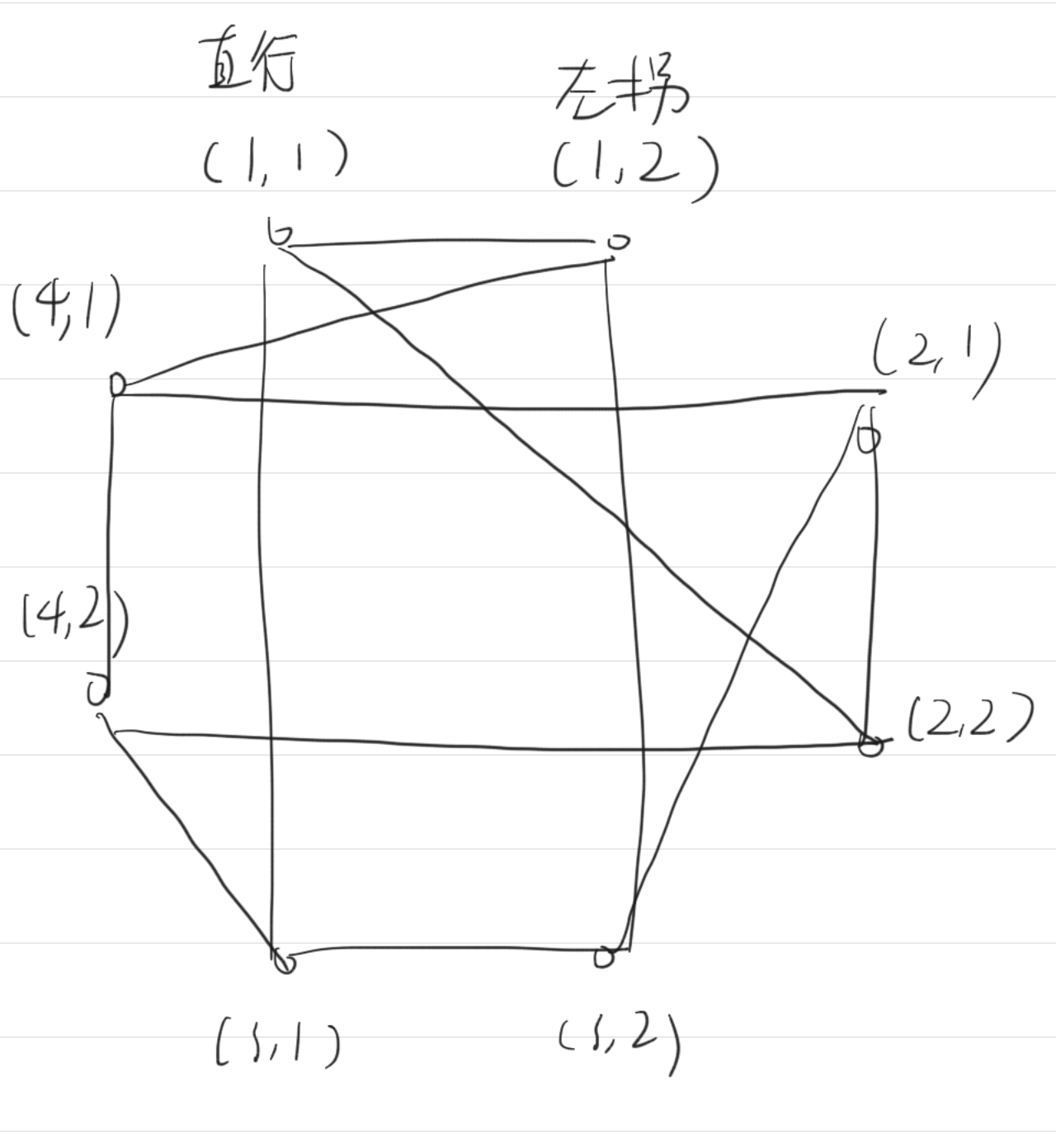
即便建出来这样一张图,还是无法想到怎么做(可以把每个车子拆出来建图用带花树,这里先不讨论这种)。这张图也不是二分图,但是我们可以通过删去两条边使之变成一张二分图,并且着两条边可以100*100地取枚举,总时间复杂度就是O(Cx100x100),C是八个点的网络流的复杂度,应该不会很大。如下图删去这两条边:
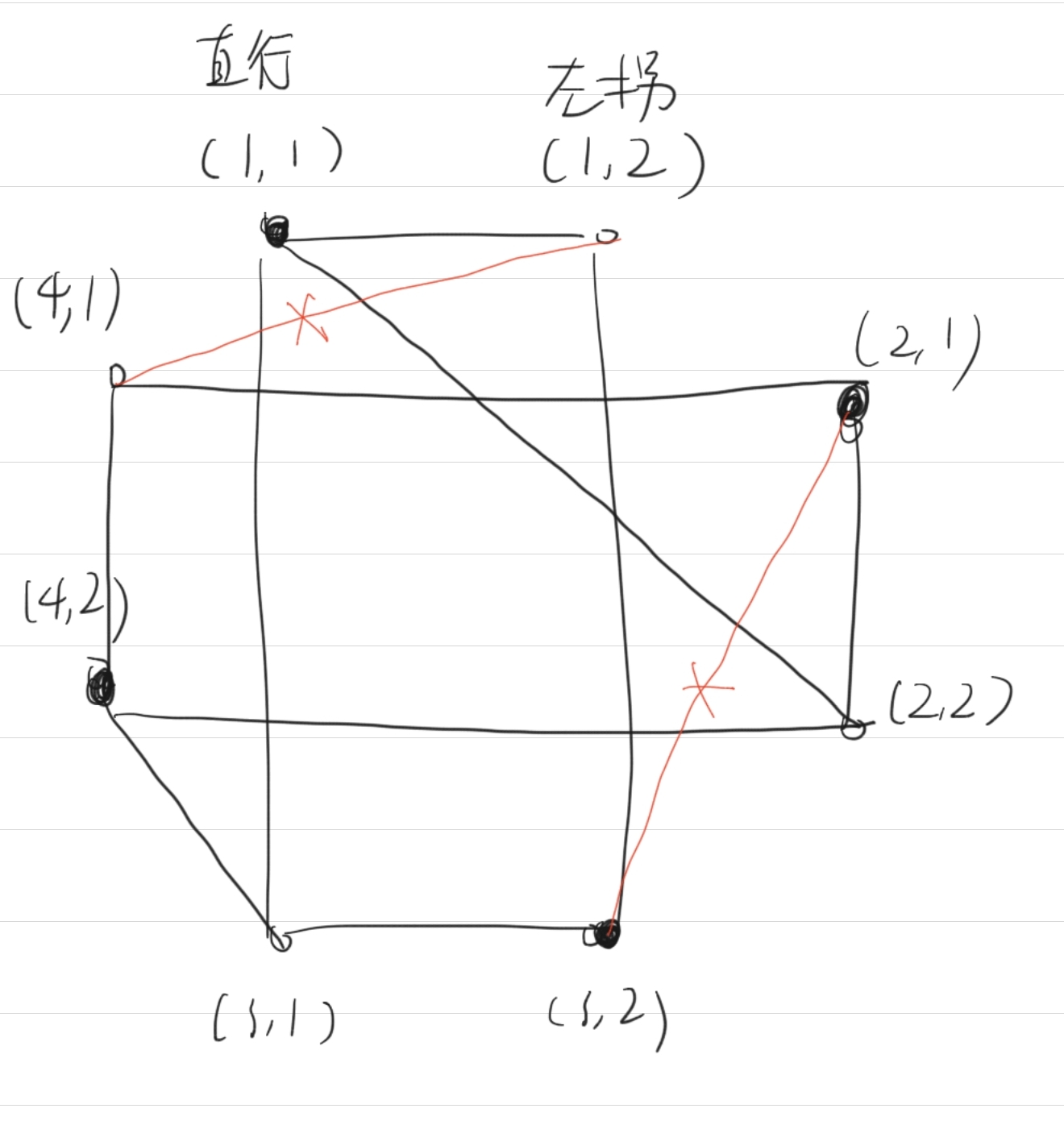
代码:(用了hjt的网络流板子)
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
int cansel_sync=(ios::sync_with_stdio(0),cin.tie(0),0);
template<class T>inline void read(T &x){x=0;char o,f=1;while(o=getchar(),o<48)if(o==45)f=-f;do x=(x<<3)+(x<<1)+(o^48);while(o=getchar(),o>47);x*=f;}
#define ll long long
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=(b);i--)
#define INF 0x3f3f3f3f
const int N = 114;
struct FLOW{
struct edge{int to,w,nxt;};
vector<edge> a; int head[N],cur[N];
int n,s,t;
queue<int> q; bool inque[N];
int dep[N];
void ae(int x,int y,int w){ // add edge
a.push_back({y,w,head[x]});
head[x]=a.size()-1;
}
bool bfs(){ // get dep[]
fill(dep,dep+n,INF); dep[s]=0;
copy(head,head+n,cur);
q=queue<int>(); q.push(s);
while(!q.empty()){
int x=q.front(); q.pop(); inque[x]=0;
for(int i=head[x];i!=-1;i=a[i].nxt){
int p=a[i].to;
if(dep[p]>dep[x]+1 && a[i].w){
dep[p]=dep[x]+1;
if(inque[p]==0){
inque[p]=1;
q.push(p);
}
}
}
}
return dep[t]!=INF;
}
int dfs(int x,int flow){ // extend
int now,ans=0;
if(x==t)return flow;
for(int &i=cur[x];i!=-1;i=a[i].nxt){
int p=a[i].to;
if(a[i].w && dep[p]==dep[x]+1)
if((now=dfs(p,min(flow,a[i].w)))){
a[i].w-=now;
a[i^1].w+=now;
ans+=now,flow-=now;
if(flow==0)break;
}
}
return ans;
}
void init(int _n){
n=_n+1; a.clear();
fill(head,head+n,-1);
fill(inque,inque+n,0);
}
int solve(int _s,int _t){ // return max flow
s=_s,t=_t;
int ans=0;
while(bfs())ans+=dfs(s,INF);
return ans;
}
}flow;
void add_edge(int x,int y,int w){flow.ae(x,y,w),flow.ae(y,x,0);}
inline int mo(int x){return (x+4-1)%4+1;}
int cnt[10][6];
int c[10][6];
int l[10],r[10],al[10],ar[10];
void solve(){
rep(i,1,4)
rep(j,1,4) cin>>c[i][j];
rep(i,1,4){
cnt[i][1] = c[i][mo(i+1)];//左走
cnt[i][2] = c[i][mo(i+2)];//前走
cnt[i][3] = c[i][mo(i-1)];//右走
}
int res = 0;
rep(i,1,4) res = max(res,cnt[i][3]);
l[1] = cnt[1][1],l[2] = cnt[2][1];
l[3] = cnt[3][2],l[4] = cnt[4][2];
r[1] = cnt[1][2],r[2] = cnt[2][2];
r[3] = cnt[3][1],r[4] = cnt[4][1];
int s=99,t=100;
int fres = INF;
int eg1 = min(l[1],l[4]),eg2 = min(r[2],r[3]);
int tot = 0;//总点权
rep(i,1,4) ar[i]=r[i],al[i]=l[i],tot+=r[i]+l[i];
//cout<<"tot"<<tot<<endl;
rep(i,0,eg1){
al[1]=l[1]-i;
al[4]=l[4]-i;
rep(j,0,eg2){
flow.init(101);//s=1,t=100;
ar[2]=r[2]-j;
ar[3]=r[3]-j;
rep(i,1,4){
add_edge(s,i,al[i]);//s to l
add_edge(4+i,t,ar[i]);//r to t
add_edge(i,4+i,INF);//同侧
add_edge(i,4+mo(i+2),INF);//对面
}
add_edge(2,5,INF);
add_edge(3,8,INF);
int tmp;
fres = min(fres,tot-flow.solve(s,t)-i-j);
}
}
cout<<max(res,fres)<<endl;
}
int main(){
int z;
cin>>z;
while(z--) solve();
}


