后缀数组SA
后缀数组SA
参考
题解 P3809 【【模板】后缀排序】 - xMinh 的博客 - 洛谷博客 (luogu.com.cn)
需要维护
- sa[i]:排名为i的后缀的起点(左端点)位置
- rk[i]:起点(左端点)为i的后缀的排名
理解:rk[sa[i]] = i 和 sa[rk[i]] = i
即【排名第i的后缀】的排名为i 和 排名第【左端点为i的后缀的排名】的左端点为i
使用倍增法
一张特别形象的图: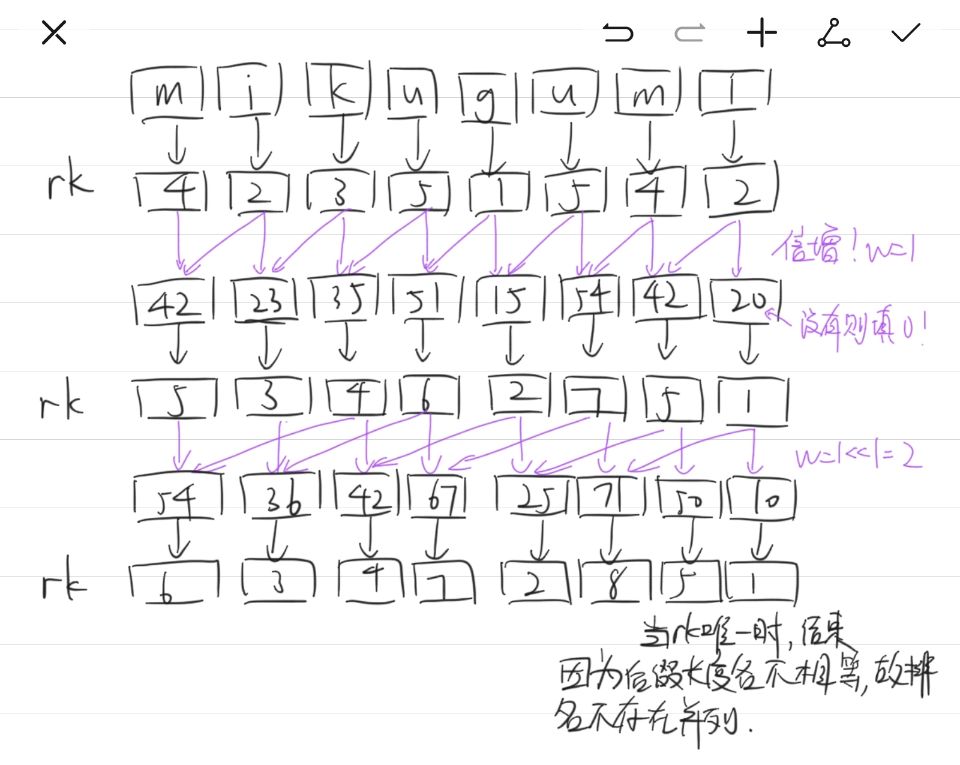
这样就能很形象的表示通过倍增进行后缀排序的过程,一直倍增直到排名各不相同为止,因为后缀的长度都不相等,所以结果肯定不会出现排名并列的情况。
图里面有个“没有则填0”是为了方便理解,在代码中应按照从左到右的顺序,先对这些没有第二关键字的后缀从左到右按顺序进行编号,作为第二关键字最小的那几个。
基数排序
一开始的序列是:21 31 32 22 23 13 12
从前往后检查低位放到对应的桶里
c[1]: 21 31
c[2]: 32 22 12
c[3]: 23 13
按照顺序取出来得到新序列:21 31 32 22 12 23 13
从前往后检查高位放入桶中
c[1]: 12 13
c[2]: 21 22 23
c[3]: 31 32
得到序列:12 13 21 22 23 31 32实现!SA学习中最大的困难竟然在基数排序
代码里,先计算了第二关键字,得到rank
rk2: 1 1 2 2 3 3 2
序列:21 31 32 22 23 13 12
之后根据第一关键字放入桶中
rk2: 3 2
c[1]: 13 12
rk2: 1 2 3
c[2]: 21 22 23
rk2: 1 2
c[3]: 31 32
最后根据第二关键字的大小,按顺序从桶中取数即可。
c[i]是前缀和,记录第一关键字<=i的一共有几个,对于拥有相同第一关键字的数,根据第二关键字从大到小取出,取出得时候分配排名为c[i],并且让c[i]--,这样之后从c[i]取数的排名就比先取的考前。代码
#include<iostream>
using namespace std;
#define ll long long
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=(b);i--)
const int MAXN = 1114514;
int n,m;
string s;
int rk[MAXN],sa[MAXN],c[MAXN],rk2[MAXN];
//sa[i]存排名i的原始编号 rk[i]存编号i的排名 第二关键字rk2
inline void get_SA(){
rep(i,1,n) ++c[rk[i]=s[i]];//基数排序
rep(i,2,m) c[i] += c[i-1];
//c做前缀和,可以知道每个关键字的排名最低在哪里
repb(i,n,1) sa[c[rk[i]]--] = i;//记录每个排名的原编号
for(int w=1;w<=n;w<<=1){//倍增
int num = 0;
rep(i,n-w+1,n) rk2[++num] = i;//没有第二关键字的排在前面
rep(i,1,n) if(sa[i]>w) rk2[++num] = sa[i]-w;
//编号sa[i]大于w的才能作为编号sa[i]-w的第二关键字
rep(i,1,m) c[i] = 0;
rep(i,1,n) ++c[rk[i]];
rep(i,2,m) c[i]+=c[i-1];
repb(i,n,1) sa[c[rk[rk2[i]]]--]=rk2[i],rk2[i]=0;
//同一个桶中按照第二关键字排序
swap(rk,rk2);
//这时候的rk2时这次排序用到的上一轮的rk,要计算出新的rk给下一轮排序
rk[sa[1]]=1,num=1;
rep(i,2,n)
rk[sa[i]] = (rk2[sa[i]]==rk2[sa[i-1]]&&rk2[sa[i]+w]==rk2[sa[i-1]+w])?num:++num;
//下一次排名的第一关键字,相同的两个元素排名也相同
if(num==n) break;//rk都唯一时,排序结束
m=num;
}
}
inline void solve(){
cin>>s;
s = ' '+s;
n = s.size()-1,m = 122;//m为字符个数'z'=122
get_SA();
rep(i,1,n) cout<<sa[i]<<' ';
cout<<endl;
}
int main(){
solve();
}
//P3809 【模板】后缀排序
//https://www.luogu.com.cn/problem/P3809最长公共前缀 LCP
Longest Common Prefix Array 最长公共前缀,LCP(i,j)表示suff(sa[i])和suff(sa[j])的最长公共前缀。
LCP的性质
- $LCP(i,j)=LCP(j,i)$
- $LCP(i,i) = length(sa[i]) = n-sa[i]+1$,起点在sa[i]的后缀,长度为n-sa[i]+1
引理
- 对任意的$k\in[i,j]$,有$LCP(i,k)=min{ LCP(i,k),LCP(k,j)}$
证明:是左右两边两个小于等于号来”夹住”的
(1)设$suff(sa[i]),suff(sa[j]),suff(sa[k])$三个串串分别是$a,b,c$
(2)设$p = min(LCP(i,k),LCP(k,j))$,则有$LCP(i,j)\geq p$。(左边夹住了)
(3)用反证法,若$LCP(i,j)\geq p+1$,因为$p = min(LCP(i,k),LCP(k,j))$,有$a[p+1]\neq b[p+1]$或$b[p+1]\neq c[p+1]$,与$a[p+1]=b[p+1]$矛盾。故征得$LCP(i,j)\leq p$
- 补充:上面的步骤(3)是摘抄自参考博客,但是有些许不严谨,可能存在$a[p+1]\neq b[p+1]$且$b[p+1]\neq c[p+1]$的情况,这样的证明漏了$a[p+1]=c[p+1]$的可能性。我的想法是:由于是经过排序后的后缀,故不等号可以修改为$<$号,即$a[p+1]< b[p+1]$或$b[p+1]<c[p+1]$,可推得$a[p+1]<c[p+1]$。
去博主下面提了一嘴w

这么一来,我们要求$LCP(i,j)$,就可以拆成$LCP(i,k),LCP(k,j)$,之后$LCP(k,j)$可以再拆,这么转化,就有点区间DP合并的感觉了
求LCP
处理height数组,$height[i]$表示$LCP(i-1,i)$,定义$height[1]=0$,这样求$LCP(i,j)$就变成了求区间最小值$min{height(x)|x\in[i+1,j]}$。但是height怎么来?
设$h[i]=height[rk[i]]$,即左端点为i的后缀的height
关键定理:$h[i]>=h[i-1]-1$
证明为摘抄,侵删
题解 P3809 【【模板】后缀排序】 - xMinh 的博客 - 洛谷博客 (luogu.com.cn)
首先我们不妨设第i-1个字符串按排名来的前面的那个字符串是第k个字符串,注意k不一定是i-2,因为第k个字符串是按字典序排名来的i-1前面那个,并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。
这时,依据height[]的定义,第k个字符串和第i-1个字符串的公共前缀自然是height[rk[i-1]],现在先讨论一下第k+1个字符串和第i个字符串的关系。
第一种情况,第k个字符串和第i-1个字符串的首字符不同,那么第k+1个字符串的排名既可能在i的前面,也可能在i的后面,但没有关系,因为height[rk[i-1]]就是0了呀,那么无论height[rk[i]]是多少都会有height[rk[i]]>=height[rk[i-1]]-1,也就是h[i]>=h[i-1]-1。
第二种情况,第k个字符串和第i-1个字符串的首字符相同,那么由于第k+1个字符串就是第k个字符串去掉首字符得到的,第i个字符串也是第i-1个字符串去掉首字符得到的,那么显然第k+1个字符串要排在第i个字符串前面。同时,第k个字符串和第i-1个字符串的最长公共前缀是height[rk[i-1]],
那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rk[i-1]]-1。
到此为止,第二种情况的证明还没有完,我们可以试想一下,对于比第i个字符串的排名更靠前的那些字符串,谁和第i个字符串的相似度最高(这里说的相似度是指最长公共前缀的长度)?显然是排名紧邻第i个字符串的那个字符串了呀,即sa[rank[i]-1]。但是我们前面求得,有一个排在i前面的字符串k+1,LCP(rk[i],rk[k+1])=height[rk[i-1]]-1;
又因为height[rk[i]]=LCP(i,i-1)>=LCP(i,k+1)
所以height[rk[i]]>=height[rk[i-1]]-1,也即h[i]>=h[i-1]-1。实现
根据上面的定理:h[i]>=h[i-1]-1 ,即height[rk[i]]>=height[rk[i-1]]-1
用k记录当前的h[i],因为h[i]>=h[i-1]-1,i每次往后移动时k–。
i从头扫到尾,k会减少n,因此我们在处理h[i]时完全可以逐字符比较,最多也只比较2n次。
int height[MAXN];
inline void get_height(){
int k = 0,j;
rep(i,1,n) rk[sa[i]] = i;
rep(i,1,n){
if(rk[i]==1) continue;//第一名往前没有前缀
if(k) k--;//h[i]>=h[i-1]-1 即height[rk[i]]>=height[rk[i-1]]-1
j = sa[rk[i]-1];//找排在rk[i]前面的
while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k]) ++k;//逐字符比较
//因为每次k只会-1,故++k最多只会加2n次
height[rk[i]] = k;
}
}写题
第一题
[P4051 JSOI2007]字符加密 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
给一个字符串,如JSOI07,对这个串的所有移动得到的串进行排序,如 JSOI07 SOI07J OI07JS I07JSO 07JSOI 7JSOI0,输出这些串按顺序排列后最后一个字母组成的串。
是很普通的一题后缀排序,把字符串复制一遍(JSOI07变成JSOI07JSOI07)再对所有的后缀进行排序即可。
#include<iostream>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=(b);i--)
const int MAXN = 114514<<2;
int n,m;
string s;
int rk[MAXN],sa[MAXN],c[MAXN],rk2[MAXN];
inline void get_SA(){
rep(i,1,n) ++c[rk[i]=s[i]];
rep(i,2,m) c[i] += c[i-1];
repb(i,n,1) sa[c[rk[i]]--] = i;
for(int w=1;w<=n;w<<=1){
int num = 0;
rep(i,n-w+1,n) rk2[++num] = i;
rep(i,1,n) if(sa[i]>w) rk2[++num] = sa[i]-w;
rep(i,1,m) c[i]=0;
rep(i,1,n) ++c[rk[i]];
rep(i,2,m) c[i] += c[i-1];
repb(i,n,1) sa[c[rk[rk2[i]]]--]=rk2[i],rk2[i]=0;
swap(rk,rk2);
rk[sa[1]]=1,num=1;
rep(i,2,n)
rk[sa[i]] = (rk2[sa[i]]==rk2[sa[i-1]]&&rk2[sa[i]+w]==rk2[sa[i-1]+w])?num:++num;
if(num==n) break;
m = num;
}
}
inline void solve(){
cin>>s;
int tmp = s.size();
s = ' '+s+s;
n = s.size()-1;m = 256;
get_SA();
rep(i,1,n)
if(sa[i]<=tmp){
//rep(j,sa[i],sa[i]+tmp-1) cout<<s[j];
//cout<<' ';
cout<<s[sa[i]+tmp-1];
}
cout<<endl;
}
int main(){
solve();
}第二题
[P4248 AHOI2013]差异 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题意:给长n(5e5)的串,问$\sum len(Ti)+len(Tj)-2\cdot LCP(Ti,Tj)|1\leq i<j\leq n$
解:首先常规的使用sa计算出height数组,之后发现这个式子的前半部分可以直接计算,即$\sum len(Ti)+len(Tj) = \frac{(n-1)n(n+1)}{2}$
后半部分$\sum LCP(Ti,Tj)$,因为有$lcp(i,j) = min(lcp(i,k),lcp(k,j))$,即$lcp(i,j) = min{height(x)|i\leq x\leq j}$故转变成 求所有区间最小值之和
所有区间最小值之和的问题,用单调栈实现即可:
维护单调栈,栈底是从$height(2)$到$height(i)$最小的元素,从底到顶单调递增
用$dp[i]$记录以$i$为右端点的所有区间的最小值之和。
对于一个新的元素$height(i)$,要找到它左边最近的比他小的元素p,在访问到$height(i)$时,把栈顶大于$height(i)$的都出栈即可。那么则有$dp[i] = dp[j]+(i-p)*height(i)$
当然,如果$height(i)$就是最小的元素,直接$dp[i] = (i-1)*height(i)$
代码:
#include<iostream>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repb(i,a,b) for(int i=(a);i>=(b);i--)
#define ll long long
const int MAXN = 114514<<3;
int n,m;
string s;
int rk[MAXN],sa[MAXN],c[MAXN],rk2[MAXN];
inline void get_SA(){
rep(i,1,n) ++c[rk[i]=s[i]];
rep(i,2,m) c[i] += c[i-1];
repb(i,n,1) sa[c[rk[i]]--] = i;
for(int w=1;w<=n;w<<=1){
int num = 0;
rep(i,n-w+1,n) rk2[++num] = i;
rep(i,1,n) if(sa[i]>w) rk2[++num] = sa[i]-w;
rep(i,1,m) c[i] = 0;
rep(i,1,n) ++c[rk[i]];
rep(i,2,m) c[i]+=c[i-1];
repb(i,n,1) sa[c[rk[rk2[i]]]--]=rk2[i],rk2[i]=0;
swap(rk,rk2);
rk[sa[1]]=1,num=1;
rep(i,2,n)
rk[sa[i]] = (rk2[sa[i]]==rk2[sa[i-1]]&&rk2[sa[i]+w]==rk2[sa[i-1]+w])?num:++num;
if(num==n) break;
m = num;
}
}
int height[MAXN];
inline void get_height(){
int k = 0,j;
rep(i,1,n) rk[sa[i]] = i;
rep(i,1,n){
if(rk[i]==1) continue;
if(k) k--;
j = sa[rk[i]-1];
while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k]) ++k;
height[rk[i]] = k;
}
}
//上面都是板子
ll res;
ll dp[MAXN];//dp[i]以i为右端点的左侧最小值之和
int stk[MAXN],ed;//单调栈
inline void solve(){
cin>>s;
n = s.length();
s = ' '+s;
m = 256;
get_SA();
get_height();
//单调栈计算所有区间的最小值之和
ed = 0;
res = (n-1)*n/2*(n+1);
rep(i,2,n){
while(0<ed&&height[stk[ed]]>=height[i]) ed--;
if(0<ed) dp[i] = dp[stk[ed]] + (i-stk[ed])*height[i];
else dp[i] = (i-1)*height[i];
stk[++ed] = i;
}
ll summ = 0;
rep(i,2,n) summ += dp[i];
res -= 2*summ;
cout<<res<<endl;
}
int main(){
solve();
}


